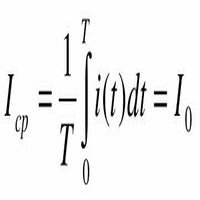Часто в цепях электронных, полупроводниковых устройств и иных ток не имеет синусоидального характера, что является для них нормой. Несинусоидальные функции являются периодическими, если выполняется условие:
i = F(t) = F(t + kT),
где Т — период функции; k — целое число.
Удобнее записывать колебания, используя замену:
Постоянные составляющие появляются в кривой тока тогда, когда присутствуют источник постоянного тока или элементы, выпрямляющие ток. При этом в несинусоидальных кривых переменного тока четные гармонические часто отсутствуют, потому что при наличии четной гармонической составляющей кривая переменного тока становится несимметричной по отношению к оси времени.
Постоянные составляющие появляются в кривой тока тогда, когда присутствуют источник постоянного тока или элементы, выпрямляющие ток. При этом в несинусоидальных кривых переменного тока четные гармонические часто отсутствуют, потому что при наличии четной гармонической составляющей кривая переменного тока становится несимметричной по отношению к оси времени. Если k четное, то cos k? = 1 и sink? = 0, тогда:
Ak sink?t + Bk cosk?t = – Ak sink?t – Bk cosk?t.
Есть единственное решение Ak = 0 и Bk = 0, значит, в кривой отсутствуют четкие гармонические составляющие.
Для расчета линейных цепей переменного тока применяют принцип наложения: ток и напряжение рассчитывают отдельно для каждой гармонической составляющей и постоянной. Для каждой из гармоник линейных цепей применяется закон Ома:
Ik = Uk / zk,
где zk — гармоническая функция порядка.