 Начнем мы, однако, с вычисления проекций момента силы на оси декартовой системы координат. При этом будем считать – для простоты – что полюсом служит начало системы координат.
Начнем мы, однако, с вычисления проекций момента силы на оси декартовой системы координат. При этом будем считать – для простоты – что полюсом служит начало системы координат.
С подобного рода циклической перестановкой мы часто сталкиваемся, когда речь заходит о координатной записи векторных произведений. Вспомните: в предыдущем пункте мы уже подвергали циклической перестановке векторы когда говорили об их попарных векторных произведениях. Формула (?) принадлежит Пуансо (1803 г.). Пуансо' , Луи (1777 – 1859) – французский механик, в трудах которого оформилась геометрическая статика. Геометрическая статика – это как раз та статика, которую Вы изучаете в данном семестре. Вы уже видели, что некоторые законы статики были сформулированы очень давно; но систематическое построение статики на основе четко сформулированных аксиом было сделано именно Пуансо в его трактате “Элементы статики”, изданном в 1803 году. С его результатами мы встретимся еще не раз.
Существует еще и аналитическая статика – раздел аналитической механики. Она возникла позднее, но относительно законченные формы приобрела не- сколько ранее, чем статика геометрическая.
Итак, статику в вузах сейчас излагают, в основном следуя Пуансо. Что изменилось с его времен? Последовательно применяется векторная символика, а в эпоху Пуансо само слово “вектор” было еще неизвестно. Впрочем, Пуансо и его современники прекрасно обходились без него, пользуясь терминами “направленный отрезок” и “геометрическое количество”. Вот только выкладки у них из-за отсутствия удобного математического формализма нередко оказывались более громоздкими, чем в современных учебниках. Предупреждаем: не коверкайте фамилию Пуансо, добавляя “н” на конце (получите “пуансон” – рабочую деталь штампа). Помните: фамилия Пуансо оканчивается на букву ... “т”: Poinsot.
Но вернемся к формуле (?). Заметим следующий факт. В правую часть формулы (?) не входит координата z. Поэтому ее значение не изменяется при сдвиге начала координат вдоль оси Oz. В самом деле, при таком сдвиге изменится только координата z, а координаты x и y не изменятся. Вывод: проекция момента силы на ось не изменяется при сдвиге полюса вдоль этой оси.
Здесь мы говорим уже не об оси Oz, а о произвольной оси: ясно, что произвольно выбранную ось в пространстве можно принять за ось Oz некоторой декартовой системы координат.
Это оправдывает введение следующего определения. Момент силы относительно оси – скалярная величина, равная проекции на эту ось момента силы относительно точки, лежащей на данной оси. Мы только что видели, что от конкретного выбора упомянутой точки ничего не меняется. Поэтому и в обозначении момента силы относительно оси можно эту точку не указывать.
Аналитический способ вычисления момента силы относительно оси мы уже рассмотрели. Рассмотрим другой – геометрический – способ такого вычисления. Формулирую соответствующий рецепт.
Геометрический способ вычисления Mz (F) :
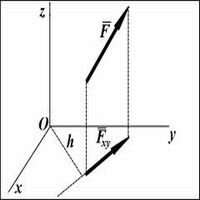
1) спроектировать вектор F и точку A на плоскость, ортогональную оси;
2) умножить модуль проекции силы на плечо этой проекции;
3) приписать произведению знак “+”, если с конца оси кратчайший поворот от BA до F виден происходящим против хода часовой стрелки, а иначе – знак “?”. Здесь над буквой F черта отсутствует. Так тоже можно писать: буква обозначает модуль вектора силы, но не сам этот вектор (направление же вектора силы показано стрелкой).
Поскольку вектор однозначно определен, когда известны его модуль и на- правление, то такой способ обозначения векторов на рисунках вполне корректен. Формула, заключенная в рамку, лежит в основе решения задач статики по теме “Плоская система сил”. Заметим еще, что для ситуации, представленной на рисунке, в формуле нужно выбрать знак “–”: сила стремится повернуть тело вокруг точки B по ходу часовой стрелки.
То, о чем мы с Вами говорили до сих пор, относилось, собственно говоря, не к статике, а лишь к ее формальному аппарату. Мы обсуждали силы и их характеристики, практически игнорируя тот факт, что силы приложены к материальным телам. Вспомним теперь, что в определении статики фигурируют также понятия равновесия и материального тела.