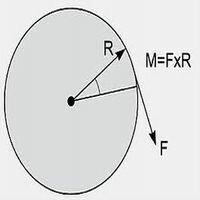
Хотя сила однозначно характеризуется своими вектором и точкой приложения, важную роль в механике играет еще одна ее характеристика. Момент силы относительно полюса B – вектор, приложенный в точке B и равный векторному произведению радиус-вектора точки приложения силы на вектор силы.
Радиус-вектор здесь, естественно, вычисляется именно относительно полюса B. Обратите внимание, что векторное произведение мы здесь будем обозначать квадратными скобками с запятой в середине. Часто используется иное обо- значение операции векторного умножения – при помощи косого креста между сомножителями.
Заметьте еще, что порядок написания сомножителей существенен: ведь Вы знаете, что при перемене мест сомножителей векторное произведение меняет знак. В определении было указано, что момент силы приложен в полюсе. Значит, это – связанный вектор.
Мы не будем указывать его точку приложения справа от символа, обозначающего момент, поскольку она уже указана в виде индекса. Рассмотрим некоторые свойства момента силы. Действительно, модуль векторного произведения равен площади параллелограмма, построенного на сомножителях; а площадь данного треугольника равна половине площади этого параллелограмма.
Далее, если вектор ортогонален двум непараллельным векторам, лежащим в одной плоскости, то он ортогонален самой этой плоскости. Строго говоря, все наши рассуждения относятся к случаю, когда треугольник не вырождается в отрезок или точку. Но в случае такого вырождения векторное произведение обращается в ноль.