ФизикаТеоретическая механика
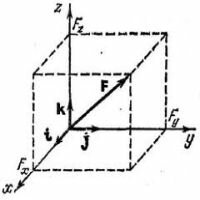В свое время мы отмечали, что если к покоящемуся абсолютно твердому телу приложить какую-либо систему сил, то оно останется в равновесии тогда и только тогда, когда эта система сил является уравновешенной. Значит, сейчас наша цель – получить простые условия, при соблюдении которых система сил будет уравновешенной.
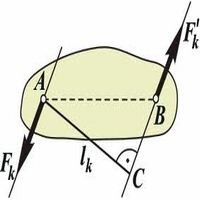Речь в этом пункте пойдет о системе из двух сил. Однако не всякая система из двух сил образует пару. Пара сил – система двух сил, равных по модулю и противоположно направленных. Из определения вытекает, что линии действия сил, образующих пару, обязательно параллельны.
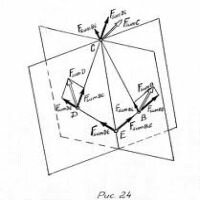Теорема. Любую систему сил при помощи элементарных операций можно привести к двум силам, одна из которых приложена в наперeд заданной точке. Уже отмечалось, что силу, вектор которой равен нулю, можно добавлять и отбрасывать, не меняя состояния тела. Такое добавление представляет собой элементарную операцию II типа.
Элементарная операция I типа – замена (по аксиоме I) двух сил, входящих в систему и приложенных к одной точке, их суммой (или разложение одной из сил на две составляющие). Сумма, стоящая справа, есть главный вектор новой системы сил. Мы видим, что он равен главному вектору старой системы сил.
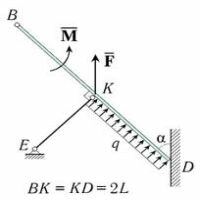Вновь начинаем с определения. Поводок – АТТ, имеющее ровно два соединения с другими телами. Поводок называется ненагруженным, если на него не действуют активные силы.
Состояние покоя материального тела (или системы тел) не нарушится, если наложить новые связи. Здесь речь идет уже не о произвольном состоянии тела, а именно о состоянии покоя. Наложение новых связей на движущееся тело может изменить характер движения.
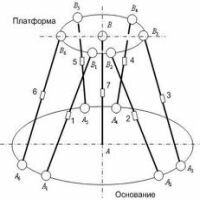Сферический шарнир – вид соединения, при котором два сочленeнных тела имеют общую точку, а других ограничений на относительное движение тел не накладывается. В частности, одно из тел может свободно поворачиваться вокруг произвольной оси, связанной с другим телом и проходящей через общую точку.
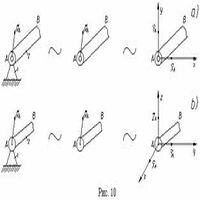Состояние тела (или системы тел) не изменится, если отбросить какие-либо из наложенных связей, заменив действие связей их реакциями. По каким правилам производится такая замена – зависит от конкретного вида отбрасываемой связи.
Начнем со следующего определения. Связь – наперeд заданное ограничение на движение тел. Обычно связи возникают при контакте абсолютно твердых тел и обусловлены способом их соединения.
Свободное АТТ под действием двух сил находится в равновесии тогда и только тогда, когда эти силы:
1) равны по модулю;
2) противоположны по направлению;
3) лежат на одной прямой.